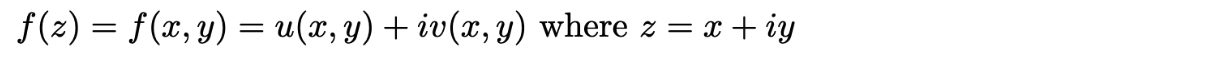Basic Fluid Dynamics
By Ryan Ng
Fluid dynamics is the field of physics that deals with modelling the behavior of fluids and gases across space. When we assume the fluid’s density to be constant in all points in space, we can model fluids using analytic functions—that is, without the help of a computer/calculator.
By modelling a fluid, we mean mapping out its properties on a 2D plane. We’re first concerned with velocity—for example, we might want to know how the water flows around a certain area. To do this, we need to introduce the concept of the velocity field.
The velocity field is a function that inputs coordinates (in our case, we’ll use 2D coordinates) and outputs a velocity vector. For example, the water’s velocity at (0, 0) might be 3 m/s to the left. We can see this as the fluid analog of the electric field. We can write this as:
The long angle brackets denote a vector. Importantly, this velocity field function does not consider time. This is because we’re assuming the fluid’s velocity at any point doesn’t change from moment to moment. This is the steady flow assumption.
This assumption is very reasonable.For example, suppose you turn on a faucet in a sink, then wait a while for the water to reach everywhere it could. After waiting enough time, the transition from having no faucet flow to having faucet flow is finished, so the water doesn’t change in velocity anywhere depending on the time. However, the velocity is different depending on location: in free space, the water is faster; when it hits a wall, however, it slows down and changes direction.
The next thing we need to introduce is the Del operator. It is defined as:
When the Del operator is applied—using the dot product—to a vector, it yields the 2D gradient (first space derivative) of the vector. When you take the dot product between the Del operator and the velocity field, we get:
Evidently, the physical meaning of the gradient of the velocity field is, it is the sum of the rate at which x-velocity increases and the rate at which y-velocity increases. Here, we have our next assumption: that the fluid is incompressible, or in other words, the density at all points is constant. This means that the above expression — ∇ • v — is equal to zero. This is clear if you see the sum of the two partial derivatives as representing the rate at which the inflow of fluid to a specific position is increasing. If ∇ • v is positive, there is more fluid entering than exiting, which means the fluid density at that point is changing.
Next, we have the irrotationality assumption, meaning that the fluid doesn’t “swirl” around any point on the field: if the fluid was water, and we put a wheel on the water stream, the wheel should not spin at all. Though a full explanation may be confusing, this is mathematically represented by
In electrostatics, while there is an electric field, there is also an electric potential: its position derivative (gradient) is the electric field. There is an analog of this for velocity—the velocity potential. Where Φ is the velocity potential, it is defined as
When we insert this into our incompressible assumption, we get
In complex analysis, there is the idea of a harmonic function, where it’s Laplacian is zero, or in other words, a function such that when the Del squared operator is applied to it, yields zero. Our velocity potential Φ fits this: it is a harmonic function. It turns out that we can bring fluid dynamics to complex analysis. In fact, we can use analytic functions!
An analytic function is a complex valued function, with complex-numbered input and output, that is complex differentiable everywhere on its domain. This is different from real differentiability, which implies that the derivative at a specific point must be the same when approaching from both the left and the right. Complex differentiability requires that the derivative at a point is the same, when approached from all directions in the complex plane—up, down, left, right, etc.
An analytic function can be written as the following, as the sum of a real and imaginary part.
All analytic functions are harmonic functions too, and it follows that its real and imaginary parts are also harmonic. What does this mean for fluid dynamics?
We would like to define a complex function where the velocity potential is the real part. In fact, knowing the real part of an analytic function, we can find its imaginary part, with the help of the Cauchy-Riemann (CR) equations. A function is analytic if and only if the CR equations are true:
where u and v are the real and imaginary parts of the complex function respectively. Defining our imaginary part as ψ, we get
As we can see, the function ψ has its gradients flipped along x and y. This means that the paths where ψ is constant are perpendicular to the paths where Φ is constant. Since we know that the latter are the equipotential lines—like in electric potential—and that they are perpendicular to the field lines (exactly like in electric fields), this shows that the paths where ψ are constant are the “streams” of fluid. ψ is the streamfunction, with this important property. Now, we can define our complex function:
While we model the Φ by modelling its gradient—the velocity field—which is (v = ∇Φ) we will be able to determine a unique function for ψ (excluding arbitrary constants), and obtain the paths of the stream. This is a powerful tool in some cases, when the incompressible assumptions actually apply, but the best part is that it’s mathematically stimulating.