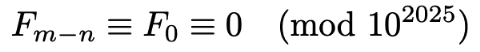Pigeonhole Principle
By Ryan Ng
Suppose I have six pigeons and five holes. I want to put all six pigeons in my five holes. Then at least one hole will have at least two pigeons.
This is pretty easy to see. If I distributed evenly to put one pigeon in each of the five holes, then I would have one pigeon left. Since all holes are full already, the last one has to share a hole with another pigeon. On the surface, this doesn’t seem that useful. But the pigeonhole principle has many applications in solving math questions.
A simple example is: if I have 13 students in a classroom, then at least two students will have their birthday in the same month. Try to prove it. I know you can. (Hint: there are 12 months in a year.)
If this seems a bit simple to you, there are two slightly more advanced versions of the pigeonhole principle.
General version
This is quite intuitive to see as well. If we distributed the pigeons evenly among the n holes, we would’ve put m pigeons in each hole equally. This would’ve housed mn pigeons. But since we have mn + 1 pigeons in total, we have 1 unhoused pigeon left, so at least one hole has m + 1 pigeons.
An example is: if I have 10 pencils to give to my 3 friends, at least one will get at least 4 pencils.
Continuous version
Feel free to prove this yourself. I believe in you!
An example for this one is: 12 scouts are on a 10 hour bus ride. At any given time, at most 6 of the scouts are asleep. Show that at least one scout must have slept for at least 5 hours.
Solution: Since at most only six were asleep at any given time, the total sleeping time between the scouts is 10 × 6 = 60. Using the pigeonhole principle, we want to split the 60 hour sleeping time into 12 people (who are the parts). 60/12 = 5, so at least one scout slept for at least 5 hours.
Applying this to problems
You would be right to notice that this seems too simple to apply to difficult math questions. The difficult part is in finding how to apply the pigeonhole principle—how to transform/spin the question so that it makes sense with pigeons and holes. A handy method is always to ask:
What is being partitioned/split into groups? (the “pigeons”)
What groups should we partition them into, to prove what’s being asked in the question? (the “holes”)
The following are some more examples. Ideally they seem cool, and hopefully you can use the pigeonhole principle to solve a problem at some point in your life. If you can, use this in a math test—it’s a great way to show off to your teachers.
Example 1: Show that, given any 5 different integers from 1 to 8, show that two of them sum to 9.
To solve this, define the “holes” as pairs of integers from 1 to 8 that sum to 9. In other words: {1, 8}, {2, 7}, {3, 6} and {4, 5}. Since we have 5 integers from 1 to 8, at least one hole (or pair of integers) will have two numbers in it. And a pair with both numbers present sums to 9.
Example 2: There is some number of people at a party (at least 2) who shake hands with each other. Show that there are two people who have shaken hands with the same number of people.
Suppose there are n people at a party. Then each person can shake hands with at most n - 1 people because you cannot shake hands with yourself. Additionally, the question requires that each person shakes hands with at least one person, so each person’s handshake count is between 1 and n - 1.
Treat all possible handshake counts as the “holes” and the people as the “pigeons”. Then there are n - 1 holes and n pigeons. So at least two people have shaken hands with the same number of people.
Example 3 (hard): Show that there exists a Fibonacci number that ends with 2025 zeros.
First, because of the pigeonhole principle, there will eventually be two numbers m and n where
where Fm and Fn are the mth and nth Fibonacci numbers. mod 10^2025 means we are looking at the remainder when both sides are divided by 10^2025. The statement means that when divided by 10^2025, both sides have the same remainder.
Second,
This is because a Fibonacci number is the sum of the previous two Fibonacci numbers.
Finally, note that the 0th Fibonacci number is 0, so its remainder when divided by 102025 is zero. Therefore:
So because the (m - n)th Fibonacci number isn’t zero, it must be a multiple of 10^2025 and therefore has 2025 trailing zeros. I think this is a great result and special honors if you managed to follow this.